Math: Quadratic Relationship
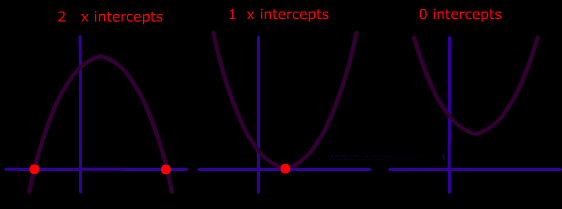
Why more then one x-intercept?
Well if you think of an parabola there can be more than 1 x-intercept and even 0 x-intercept. Well today I'm going to show you how to solve it (it's very easy).
Example:
y=2(x-5)²-50
0=2(x-5)²-50 Set y=0
0+50=2(x-5)² Bring the 50 to the other side making it postive.
50/2=2(x-5)²/2 Divide both sides by 2
√25=√(x-5)² Square root both sides
x-5=√25 Without square rooting the x bring it to the other side making it x-5.
IMPORTANT: The root on 25 has a both postive and a negative sign because (-5)² and 5² are both equal to 25 therefore there will be 2 x-intercepts.
x=√25+5 x=√25+5
x=5+5 x=-5+5
x=10 x=0 Therefore the 2 x-intercepts would be 10 and 0.
In whatever grade you probably learned order of operations or you might call it BEDMAS. When solving for the x-intercepts you do the opposite of what you learned.
For example instead of doing brackets first you do the brackets last.
When you found the x-intercepts for linear lines you probably made y=0 and then found the x-intercept so that is what you would do to find the x-intercept(s) for a parabola in vertex form.