Math: Quadratic Relationship
What is the axis of symmetry and optimal value?
If you read the other page on vertex form properly then you should know that the axis of symmetry divides the parabola into two equal halves and the optimal value is the y co-ordinate of the vertex.
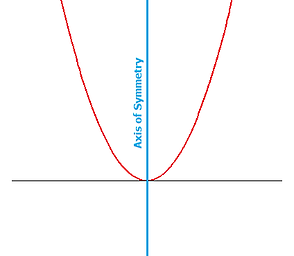
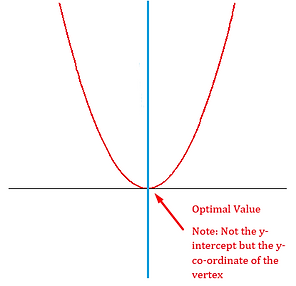
If you were to write the axis of symmetry then how would you write it?
You would have probably written it just as a number but that would be wrong.
The proper way to write axis of symmetry is x=h where the h is a number.
The axis of symmetry is x=h which means that it will always be the h value of the vertex.
If you were to write the optimal value then how would you write it?
You would have probably written it just as a number but that would be wrong.
The proper way to write the optimal value is y=k where the k is a number.
The optimal value is y=k which means that it will always be the k value of the vertex.
The optimal value is also the maximum or minimum value of a parabola. If the parabola opens downwards then it would have a maximum value (highest point) and if the parabola opens upwards then it would have a minimum value (lowest point).
Can we figure out if the parabola has a maximum or minimum value just by looking at the equation?
Yes, we can tell that easily if the equation is in vertex form. If the a value of the equation is postive then it would have a minimum value and if the a value is negative then it would have a maximum value.
EXAMPLES:
y=0,5(x-4)²+5
The axis of symmetry would be x=4 and the optimal value would be y=5
y=-3(x+2)²-7
The axis of symmetry would be x=-2 and the optimal value would be y=-7